Le bon sens le sait : il ne faut pas faire d’un cas une généralité. Pour autant, peut-on faire une généralité à partir de 2 cas ? de 10 cas ? de 20 cas ? On « sent bien» que plus il y aura de cas, plus notre généralité aura de chances d’être juste… cependant, pour que ce soit le cas, il y a deux conditions importantes à remplir : 1-avoir « assez » d’individus, et 2- que ces individus soient représentatifs.
1- Avoir des individus représentatifs
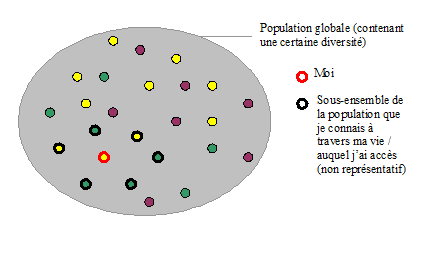
Règle number one, très très importante : vous aurez beau avoir 1 million de cas, ils n’auront absolument aucune valeur si ces cas ne sont pas représentatifs de l’ensemble sur lequel vous voulez tirer une généralité.
Représentatif, ça veut dire quoi ? Cela signifie que les individus de mon échantillon doivent représenter la diversité des individus qui existent dans la population. Par exemple, si je veux étudier la taille des français, je dois faire mes mesures sur les français en général, donc avoir des grands, des petits, des moyens, et ce dans des proportions équivalentes à celles de la population française. En gros, si je dessinais la cloche des tailles à partir de mon échantillon d’individus, je dois obtenir à peu près la même que si j’avais mesuré la taille de tous les français sans exception.
Si je vais sur un chantier, et que je mesure tous les hommes présents, ma mesure me donnera une idée de la taille moyenne de l’ouvrier à l’endroit où j’ai été. Je n’ai pas le droit de généraliser à l’ensemble des hommes français, et encore moins à l’ensemble des français tout court (hommes et femmes). En effet, les hommes sont en moyenne plus grands que les femmes, donc en ayant un échantillon qui n’est formé que d’hommes, je surestimerais la taille moyenne de la population française. On dit que si l’échantillon n’est pas représentatif, notre « estimation» de la taille moyenne est biaisée.
Pour obtenir un échantillon représentatif, il existe des méthodes. Je ne vais pas rentrer dans les détails techniques, mais il y a une règle à connaître : plus les individus sont sélectionnés au hasard, mieux c’est. Ainsi, la meilleure de toutes les méthodes, dans l’idéal, serait d’avoir la liste de tous les français, et de tirer le nombre d’individus que l’on souhaite au hasard dans cette liste. Ainsi, on aura des individus de tout genre, toute origine sociale, tout age, etc. Ils seront représentatifs de la population française.
Lorsque l’on fait de son cas (ou des quelques cas qu’on a croisé dans sa vie…) une généralité, on risque très fort de ne pas avoir un échantillon représentatif, mais un échantillon biaisé. En effet, en tant qu’individu, qui que l’on soit, au minimum, on côtoie un certain milieu social spécifique, on a accès ou non à certains services, on ne vit qu’à un seul endroit à la fois. Qui que l’on soit, on n’a donc accès qu’à une partie restreinte de la population, et on ne devrait donc jamais faire de généralités à partir de nos observations « personnelles». Ca ne veut pas dire que les observations personnelles n’ont aucune valeur. Elles permettent de formuler des hypothèses… qu’on pourra ensuite tester avec la méthode scientifique.
(Ou vérifier en consultant -vive internet- ce qu’en disent les études qui les ont testé… jetez déjà un œil à la compilation de Tatoufaux, vous verrez sans doute, comme moi, quelques unes des « généralités» que vous croyiez belles et bien acquises tomber à l’eau…).

2- Avoir assez d’individus
C’est la grande question que posent absolument tous les étudiants en science lors de leur premier stage de recherche, quand ils doivent mettre au point leur tout premier protocole expérimental : combien de « réplications » (=cas) doivent-ils prévoir (c’est-à-dire, si c’est une expérience sur les rats, par exemple, combien de rats)? A tous, on répond la même chose : « Ca dépend» ! Très frustrant, comme réponse, n’est ce pas ?
Et pourtant, là n’est pas le pire, il y a encore plus frustrant : le nombre d’individus qu’il faut, ça dépend des données elles-mêmes… donc on ne peut le mesurer qu’après l’expérience… quand on a les données. Du coup, on ne sait pas si on a prévu assez de réplications tant qu’on n’a pas terminé la recherche, et fait quelques calculs.
Alors, quels calculs ? De quoi « ça dépend» le nombre d’individus qu’il faut ? On l’a dit, pour avoir un échantillon représentatif, la meilleure méthode est de tirer les individus au hasard. Cependant, même en tirant les individus au hasard, il existe un risque, en étant très malchanceux, que l’échantillon obtenu soit très différent, dans sa composition, de la population sur laquelle on veut faire une généralité. Pour mieux comprendre, imaginons : j’ai une population d’allemand, et d’après un recensement, je sais que la moitié d’entre eux, très exactement, aime les fraises (j’admets, c’est une question bizarre pour un recensement, mais c’est pour l’exemple, il faut faire preuve d’ouverture d’esprit).
Je veux savoir si pour les français c’est pareil, si la moitié d’entre eux aime les fraises.
Je tire 10 français au hasard. Si effectivement comme pour les allemands, la moitié aime les fraises, j’ai de bonnes chances d’avoir environ la moitié de mes dix individus tirés au hasard qui aiment les fraises. Si j’en conclue que les français sont comme les allemands (ie que la moitié des français aiment les fraises), j’ai de la chance, j’ai bon.
Mais j’ai aussi une probabilité non nulle de ne tirer, par malchance, que des français qui aiment les fraises, ou que des français qui n’aiment pas les fraises. Et là, si je conclue que les français sont différents des allemands, pas de bol, j’ai faux.
Encore une frustration : même en ayant tout bien fait comme il faut pour avoir un échantillon représentatif (c’est-à-dire même en ayant utilisé le hasard), il y a un risque de tirer de mauvaises conclusions, un risque d’erreur.
L’énorme différence entre l’erreur et le biais (le biais c’est ce qu’on a vu en 1ere partie, faut suivre), c’est qu’avec le biais, on ne sait jamais à quel point on se trompe dans nos conclusions… et ça, c’est pas bon. L’erreur, par contre, on peut calculer sa probabilité. Par exemple, pour les français qui aiment ou non les fraises, on peut calculer la probabilité de tirer autant de français qui aiment les fraises alors qu’il y avait moitié-moitié dans la population… cette probabilité, c’est (environ) 1/210 (1/2 car on a une chance sur deux de tirer un individu qui aime les fraise à chaque tirage, et exposant 10 car on fait dix tirages), soit (environ) 0,001, soit 0,1%. En gros, il aurait été très improbable (moins d’une chance sur 100) de ne tirer que des individus qui aiment les fraises s’il y avait moitié-moitié. Si je ne tire que des individus qui aiment les fraises, je prends donc un risque plutôt faible en concluant qu’il n’y a pas moitié-moitié dans la population, donc que les français sont différents des allemands. Dans le cas présent, 10 individus étaient suffisants pour tirer une conclusion.
Je reformule, pour être sure que le message passe: on aura toujours un risque, à cause du hasard, de faire une fausse conclusion. Mais ce risque, on peut le calculer. S’il est faible, on pourra conclure, donc c’est qu’on avait prévu assez d’individus dans notre échantillon.
Si je n’avais tiré que 4 individus, et que tous aimaient les fraises, la probabilité aurait été de 1/24 soit environ 6%… c’est déjà un risque plus important, qu’on est pas forcément prêt à prendre… on fera alors une nouvelle étude, avec plus d’individus, pour avoir un risque plus « acceptable» avant de tirer une conclusion.
Lorsque l’on fait de son cas une généralité, on a bien souvent aucune idée du nombre d’individus qu’il aurait fallu pour conclure… donc du risque qu’on prend de se tromper. Encore un argument pour préférer la méthode scientifique à l’approche individuelle.
Publié originellement le 7 avr. 2015 et republié le 07 mars 2018 suite à migration du site.
Article reproduit avec l’aimable autorisation de l’autrice, publié originellement sur Ce n’est qu’une théorie